Interesting Surfaces

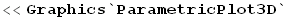
Algebraic and parametric surfaces introduced in "http://www.uib.no/People/nfytn/mathgal.htm"
are drawn using Mathematica 4.2

Algebraic Cylinders

$ImplicitPlot3D[2 x^4 - 3 x^2 y + y^2 - 2 y^3 + y^4 == 0, {x, -4, 4}, {y, -4, 4}, {z, -2, 2}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_4.gif]

Astrodal Ellipsoid

$a = 1 ; b = 1 ; c = 1 ; ParametricPlot3D[{(a Cos[u] Cos[v])^3, (a Sin[u] Cos[v])^3, (c Sin[v])^3}, {u, -Î, Î}, {v, -Î, Î}, Boxed -> False, Axes -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_6.gif]

Barth Sextic

$t = 0.5 (1 + 5^(1/2)) ; ImplicitPlot3D[4 (t^2 x^2 - y^2) (t^2 y^2 - z^2) (t^2 z^2 - z^2) - (1 ... + z^2 - 1)^2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, PlotPoints -> 30, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_8.gif]

Barth Decic

$t = 0.5 (1 + 5^(1/2)) ; w = 1 ; ImplicitPlot3D[8 (x^2 - t^4 y^2) (y^2 - t^4 z^2) (z^2 - t^4 x^ ... (x^2 + y^2 + z^2 - (2 - t) w^2)^2 == 0, {x, -4, 4}, {y, -4, 4}, {z, -4, 4}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_10.gif]

Bicorn

$ImplicitPlot3D[y^2 (1 - (x^2 + z^2)) - (x^2 + z^2)^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_12.gif]

Bifolia

$a = 3 ; ImplicitPlot3D[(x^2 + y^2 + z^2)^2 - a (z^2 + z^2) y == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_14.gif]

Bohemian Dome

[Graphics:HTMLFiles/InterestingSurfaces_16.gif]

Boy Surface

$ImplicitPlot3D[64 (1 - z)^3 z^3 - 48 (1 - z)^2 z^2 (3 x^2 + 3 y^2 + 2 z^2) + 12 (1 - z) z (27 ... y^2) + 4 z^4) == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 50] ;$

[Graphics:HTMLFiles/InterestingSurfaces_18.gif]

Cassini Ovals

$a = 0.45 ; b = 0.5 ; c = 16 ; ImplicitPlot3D[(x^2 + y^2 + z^2 + a^2)^2 - c a^2 (z^2 + z^2 - b^2) == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_20.gif]

Cayley cubic

$ImplicitPlot3D[-5 (x^2 y + x^2 z + y^2 x + y^2 z + z^2 y + z^2 x) + 2 (x y + x z + y z) == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_22.gif]

Chair

$k = 5 ; a = 0.95 ; b = 0.8 ; ImplicitPlot3D[(x^2 + y^2 + z^2 - a k^2)^2 - b ((z - k)^2 - 2 x^2 ... k)^2 - 2 y^2) == 0, {x, -4, 4}, {y, -4, 4}, {z, -4, 4}, Boxed -> False, PlotPoints -> 40] ;$

[Graphics:HTMLFiles/InterestingSurfaces_24.gif]

Crossed Trough

$ImplicitPlot3D[x^2 z^2 - y == 0, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_26.gif]

Cuibic Saddle

$ImplicitPlot3D[x^3 - y^3 - z == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_28.gif]

Cushion

$ImplicitPlot3D[z^2 x^2 - z^4 - 2 z x^2 + 2 z^3 + x^2 - z^2 - (x^2 - z)^2 - y^4 - 2 x^2 y^2 - y ... 2 y^2 z + y^2 == 0, {x, -4, 4}, {y, -3, 3}, {z, -4, 4}, Boxed -> False, PlotPoints -> 60] ;$

[Graphics:HTMLFiles/InterestingSurfaces_30.gif]

Dervish

$a = 1/5 (-8) (1 + 1/5^(1/2)) (5 - 5^(1/2))^(1/2) ; c = (5 - 5^(1/2))^(1/2)/2 ; ImplicitPlot3D[ ... (1/2)) z^2)^2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 40] ;$

[Graphics:HTMLFiles/InterestingSurfaces_32.gif]

Devil's Curve Variant

$ImplicitPlot3D[x^4 + 2 x^2 z^2 - 0.36 x^2 - y^4 + 0.25 y^2 + z^4 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 40] ;$

[Graphics:HTMLFiles/InterestingSurfaces_34.gif]

Dini's Surface

[Graphics:HTMLFiles/InterestingSurfaces_36.gif]

Dupin Cyclid

double crescent

$r0 = 4.9 ; r1 = 5 ; dx = 2 ; dy = 0 ; ri = 3 ; ImplicitPlot3D[(r1^2 - dy^2 - (dx + r0)^2) (r1^ ... ^2 y^2 + ri^8 == 0, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_38.gif]

degenerate w.arch

$r0 = 3 ; r1 = 5 ; dx = 3 ; dy = 0 ; ri = 9 ; ImplicitPlot3D[(r1^2 - dy^2 - (dx + r0)^2) (r1^2 ... + ri^8 == 0, {x, -30, 30}, {y, -30, 30}, {z, -30, 30}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_40.gif]

plain

$r0 = 6 ; r1 = 0.5 ; dx = 3 ; dy = 0 ; ri = 12 ; ImplicitPlot3D[(r1^2 - dy^2 - (dx + r0)^2) (r1 ... + ri^8 == 0, {x, -30, 30}, {y, -50, 20}, {z, -30, 30}, Boxed -> False, PlotPoints -> 50] ;$

[Graphics:HTMLFiles/InterestingSurfaces_42.gif]

Ennepers Surface

$ParametricPlot3D[{u - u^3/3 + u v^2, v - v^3/v + u^2 v, u^2 - v^2}, {u, -2, 2}, {v, -2, 2}, Boxed -> False, Axes -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_44.gif]

Folium Surface

$a = 1 ; b = 1 ; ImplicitPlot3D[(y^2 + z^2) (1 + (b - 4 a) x) + x^2 (1 + b) == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_46.gif]

Glob

$ImplicitPlot3D[0.5 x^5 + 0.5 x^4 - (y^2 + z^2) == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_48.gif]

Heart

$ImplicitPlot3D[(2 x^2 + y^2 + z^2 - 1)^3 - (x^2 z^3)/10 - y^2 z^3 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 3}, Boxed -> False, PlotPoints -> 100, ViewPoint -> {2.5, 1, 1}] ;$

[Graphics:HTMLFiles/InterestingSurfaces_50.gif]

Hunt Surface

$ImplicitPlot3D[4 (x^2 + y^2 + z^2 - 13)^3 + 27 (3 x^2 + y^2 - 4 z^2 - 12)^2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_52.gif]

Hyperbolic Torus

$r0 = 0.6 ; r1 = 0.4 ; ImplicitPlot3D[x^4 + 2 x^2 y^2 - 2 x^2 z^2 - 2 (r0^2 + r1^2) x^2 + y^4 - ... r0^2 - r1^2)^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_54.gif]

Kampyle of Eudoxus

$a = 0.2 ; c = 1 ; ImplicitPlot3D[(y^2 + z^2) - c^2 x^4 + c^2 a^2 x^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_56.gif]

Kline Bottle

$ParametricPlot3D[{Cos[u] (Cos[u/2] (2^(1/2) + Cos[v]) + Sin[u/2] Sin[v] Cos[v]), Sin[u] (Cos[u ... , {u, 0, 4 Î}, {v, 0, 2 Î}, Boxed -> False, Axes -> False, PlotPoints -> 100] ;$

[Graphics:HTMLFiles/InterestingSurfaces_58.gif]

$ImplicitPlot3D[(x^2 + y^2 + z^2 + 2 y - 1) ((x^2 + y^2 + z^2 - 2 y - 1)^2 - 8 z^2) + 16 x z (x ... 5}, {y, -5, 5}, {z, -5, 5}, Boxed -> False, PlotPoints -> 100, ViewPoint -> {4, 1, 1}] ;$

[Graphics:HTMLFiles/InterestingSurfaces_60.gif]

Kuen's Surface

$ParametricPlot3D[{(2 (Cos[u] + u Sin[u]) Sin[v])/(1 + u^2 Sin[v]^2), (2 (Sin[u] + u Cos[u]) Si ... {u, -4, 4}, {v, 0.05, Î - 0.05}, Boxed -> False, Axes -> False, PlotPoints -> 100] ;$

[Graphics:HTMLFiles/InterestingSurfaces_62.gif]

Kummer Surface

$ImplicitPlot3D[x^4 + y^4 + z^4 - x^2 - y^2 - z^2 - x^2 y^2 - x^2 z^2 - y^2 z^2 + 1 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 50] ;$

[Graphics:HTMLFiles/InterestingSurfaces_64.gif]

Lemniscate of Gerono, or Eight Curve

$ImplicitPlot3D[x^4 - x^2 + y^2 + z^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_66.gif]

Mitre Surface

$ImplicitPlot3D[4 x^2 (x^2 + y^2 + z^2) - y^2 (1 - y^2 - z^2) == 0, {x, -1, 1}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_68.gif]

Moebius Strip

[Graphics:HTMLFiles/InterestingSurfaces_70.gif]

Nodal_Cubic

$ImplicitPlot3D[y^3 + z^3 - 6 y z == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_72.gif]

Odd Surface

$ImplicitPlot3D[z^2 x^2 - z^4 - 2 z x^2 + 2 z^3 + x^2 - z^2 - (x^2 - z)^2 - y^4 - 2 ... 2 y^2 z + y^2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 100] ;$

[Graphics:HTMLFiles/InterestingSurfaces_74.gif]

Paraboloid

$ImplicitPlot3D[x^2 - y + z^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_76.gif]

Parabolic Torus

$r0 = 0.6 ; r1 = 0.5 ; ImplicitPlot3D[x^4 + 2 x^2 y^2 - 2 x^2 z - (r0^2 + r1^2) x^2 + y^4 - 2 y ... r0^2 - r1^2)^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 50] ;$

[Graphics:HTMLFiles/InterestingSurfaces_78.gif]

Pillow/Tooth Object

$ImplicitPlot3D[x^4 + y^4 + z^4 - (x^2 + y^2 + z^2) == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 50] ;$

[Graphics:HTMLFiles/InterestingSurfaces_80.gif]

Piriform

$ImplicitPlot3D[(x^4 - x^3) + y^2 + z^2 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_82.gif]

Quartic Paraboloid

$ImplicitPlot3D[x^4 + z^4 - y == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_84.gif]

Quartic Saddle

$ImplicitPlot3D[x^4 - z^4 - y == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_86.gif]

Steiners Roman Surface

$ImplicitPlot3D[x^2 y^2 + x^2 z^2 + y^2 z^2 + x y z == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False, PlotPoints -> 100] ;$

[Graphics:HTMLFiles/InterestingSurfaces_88.gif]

Strophoid

$a = 1 ; b = -0.1 ; c = 0.8 ; ImplicitPlot3D[(b - x) (y^2 + z^2) - c^2 a x^2 - c^2 x^3 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_90.gif]

Right Strophoid

$a = 1 ; b = 1 ; c = 0.8 ; ImplicitPlot3D[(b - x) (y^2 + z^2) - c^2 a x^2 - c^2 x^3 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_92.gif]

Trisectrix of Maclaurin

$a = 1 ; b = 1/3 ; c = 0.8 ; ImplicitPlot3D[(b - x) (y^2 + z^2) - c^2 a x^2 - c^2 x^3 == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_94.gif]

Swallowtail

$ParametricPlot3D[{u v^2 + 3 v^4, -2 u v - 4 v^3, u}, {u, -2, 2}, {v, -0.8, 0.8}, Boxed -> False, Axes -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_96.gif]

Tangle

$ImplicitPlot3D[x^4 - 5 x^2 + y^4 - 5 y^2 + z^4 - 5 z^2 + 11.8 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 100] ;$

[Graphics:HTMLFiles/InterestingSurfaces_98.gif]

Torus

$r0 = 1 ; r1 = 0.5 ; ImplicitPlot3D[x^4 + y^4 + z^4 + 2 x^2 y^2 + 2 x^2 z^2 + 2 y^2 z^2 - 2 (r0 ... r0^2 - r1^2)^2 == 0, {x, -2, 2}, {y, -2, 2}, {z, -2, 2}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_100.gif]

Umblrella

$ImplicitPlot3D[x^2 - y z^2 == 0, {x, -3, 3}, {y, 0, 6}, {z, -3, 3}, Boxed -> False, PlotPoints -> 30] ;$

[Graphics:HTMLFiles/InterestingSurfaces_102.gif]

Witch of Agnesi

$a = 0.04 ; ImplicitPlot3D[a (y - 1) + (x^2 + z^2) y == 0, {x, -1, 1}, {y, -1, 1}, {z, -1, 1}, Boxed -> False] ;$

[Graphics:HTMLFiles/InterestingSurfaces_104.gif]

Converted by Mathematica (September 25, 2003)